12 Ciekawostek o Wielokątach Foremnych

Wielokąty foremne należą do tej grupy wielokątów u których wszystkie boki są takiej samej długości oraz kąty wewnętrzne są sobie równe. Figury te zawsze są wypukłe. Zajmował się nimi wybitny niemiecki matematyk Carl Friedrich Gauss. Jego odkryciem było stwierdzenie, iż każdy n-kąt foremny można bez najmniejszego problemu skonstruować za pomocą linijki i cyrkla, choć musi być spełniony warunek związany z liczbami Fermata. Miało to miejsce w 1801 roku.

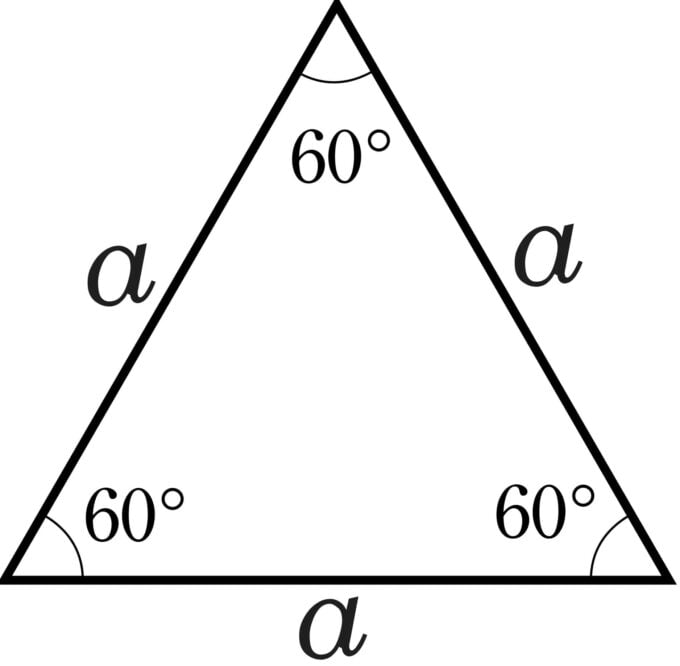
1. Mówiąc o wielokątach foremnych wiele osób wyobraża sobie dosyć skomplikowane figury o większej ilości boków. Tymczasem wielokątem o najmniejszej ilości boków jest trójkąt równoboczny. Spełnia absolutnie wszystkie warunki, by zasilać grono wielokątów foremnych. Podobna sytuacja dotyczy kwadratu.

2. Specyficzna konstrukcja wielokątów foremnych sprawia, że włąściwie na każdym z nich można opisać okrąg. Co więcej, wewnątrz figury można także wpisać okrąg. Warto dodać, że ich środki będą zawsze w tym samym miejscu.

3. W przypadku trójkąta równobocznego miara kąta wewnętrznego wynosi 60 stopni, w kwadratach 90 stopni, w pięciokątach 108 stopni, a w sześciokątach 120 stopni.

4. Wielokątem foremnym nie są figury, w których kąty odznaczają się różnymi miarami. Przykładem figury nie należącej do grona wielokątów foremnych jest romb.

5. Ciekawostką jest, że promień wpisanego w kwadrat okręgu zawsze będzie połową długości boku kwadratu.

6. Wielokąty foremne od dawna zachwycają i to nie tylko matematyków swoim perfekcyjnym kształtem. Bywają również niemałą inspiracją dla architektów. W 1941 roku rozpoczęła się budowa jednego z najbardziej charakterystycznych budynków W Stanach Zjednoczonych. Mowa oczywiście o Departamencie Obrony – budynku w kształcie idealnego pięciokąta. Mówi się, że kształt wynika przede wszystkim z układu drogowego w okolicy.

7. Wielokąty foremne pojawiają się od stuleci również w sztuce, stając się sposobem na wyrażenie myśli artysty. Przykładem może być bardzo głośny obraz Kazimierza Malewicza. Dzieło nazywane „Czarnym kwadratem na białym tle” faktycznie przedstawia kwadrat na białym tle i nic poza tym. Mimo wszystko, zostało uznane za jedno z najważniejszych w dorobku artysty.

8. Nazwa kwadrat pochodzi od łacińskiego słowa quadratus, które oznacza równoboczny. Warto wiedzieć, że ta figura już w starożytnym Egipcie stanowiła jedną z najważniejszych jednostek pola. Matematyka nie sprawiała ówczesnym ludziom większych problemów, biorąc pod uwagę niesamwite pozostałości w postaci, np. piramid czy innych świątyń.

9. Trójkąty równoboczne znalazły zastosowanie między innymi w ruchu drogowym. Charajterystyczny kształt znaków ostrzegawczych zwraca uwagę kierowców na ewentualne niebezpieczeństwo. Jedynym w swoim rodzaju znakiem jest znak STOP, który tak de facto jest ośmiokątem. Pozwala on dostrzec znak nawet w sytuacji, gdy sama plansza nie jest widoczna, np. z powodu opadów śniegu.

10. Od dawna mówi się, że matematyka ma swoje źródła w naturze. Faktycznie jej przejawy są obecne niemal na każdym roku, ale nie sposób się temu dziwić, skoro jest królową wszystkich nauk. Przykładem mogą być idealne plastry miodu, które mają kształ heksagonów, czyli sześciokątów.

11. Nie sposób wyobrazić sobie wielu dziedzin bez wielokątów foremnych. Pojawiają się w rozmiatych odsłonach i tak naprawdę doświadczamy ich obecności każdego dnia.

12. Zwiększanie ilości boków w przypadku wielokątów foremnych oznacza, że figura w pewnym momencie zaczyna przypominać koło.