14 intrygujących ciekawostek o liczbie e
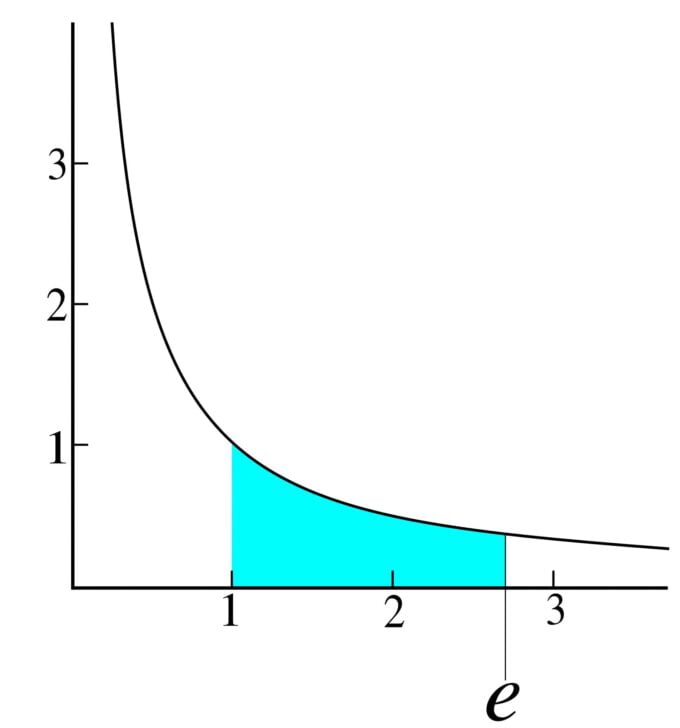
Podobnie jak pi, e jest niewymierną liczbą rzeczywistą. Oznacza to, że nie można go zapisać jako ułamek, a jego rozwinięcie dziesiętne trwa w nieskończoność bez powtarzającego się bloku liczb, który ciągle się powtarza.
1. Liczba e jest również transcendentalna, co oznacza, że nie jest pierwiastkiem niezerowego wielomianu o wymiernych współczynnikach. Pierwsze pięćdziesiąt miejsc po przecinku jest podane przez e = 2,718281828459045235360287471352662497757724709369995
2. Liczba e została odkryta przez ludzi, którzy byli ciekawi oprocentowania składanego. W tej formie odsetek zleceniodawca zarabia odsetki, a następnie wygenerowane odsetki same na siebie zarabiają. Zaobserwowano, że im większa częstotliwość okresów kapitalizacji w roku, tym wyższa kwota wygenerowanych odsetek.
3. Liczba e jest stosowana w matematyce. Oto kilka miejsc, w których się pojawia: Jest to podstawa logarytmu naturalnego. Ponieważ Napier wynalazł logarytmy, e jest czasami określane jako stała Napiera.
4. W rachunku różniczkowym funkcja wykładnicza ex ma unikalną właściwość bycia własną pochodną.
5. Wyrażenia z udziałem ex i e-x łączą się, tworząc hiperboliczne funkcje sinusa i hiperbolicznego cosinusa.
6. Dzięki pracy Eulera wiemy, że podstawowe stałe matematyki są powiązane wzorem eiΠ +1=0, gdzie i jest liczbą urojoną będącą pierwiastkiem kwadratowym z jedynki ujemnej.
7. Liczba e pojawia się w różnych formułach w matematyce, zwłaszcza w obszarze teorii liczb.
8. Znaczenie liczby e nie ogranicza się do kilku dziedzin matematyki. Istnieje również kilka zastosowań liczby e w statystyce i prawdopodobieństwie.
9. Liczba e pojawia się we wzorze na funkcję gamma. Wzory na standardowy rozkład normalny obejmują e do potęgi ujemnej. Ta formuła zawiera również pi.
10. Wiele innych dystrybucji wymaga użycia liczby e. Na przykład wszystkie wzory na rozkład t, rozkład gamma i rozkład chi-kwadrat zawierają liczbę e.
11. Pierwszy krok do odkrycia e zaczyna się od jednego szkockiego polimata: Johna Napiera. O wiele wygodniejsze wymyślanie niż teoretyzowanie, wkład Napiera nie wynika z ostrej czystej matematyki, ale bardziej z praktycznej potrzeby: skrótu obliczeniowego przy mnożeniu bardzo dużych liczb.
12. Istnieje wiele sposobów obliczania wartości e, ale żaden z nich nigdy nie daje całkowicie dokładnej odpowiedzi, ponieważ e jest irracjonalne, a jego cyfry trwają w nieskończoność, nie powtarzając się. Ale znana jest z ponad 1 bilionem cyfr dokładności!
13. Jeśli poprosisz kogoś o nazwanie swojej ulubionej stałej matematycznej, prawdopodobnie otrzymasz zagadkowe spojrzenia. Po chwili ktoś może zgłosić, że najlepszą stałą jest pi. Ale to nie jedyna ważna stała matematyczna. Bliskim drugim, jeśli nie pretendentem do korony najbardziej wszechobecnej stałej jest e. Liczba ta pojawia się w rachunku różniczkowym, teorii liczb, prawdopodobieństwie i statystyce. Zbadamy niektóre cechy tej niezwykłej liczby i zobaczymy, jakie ma ona powiązania ze statystykami i prawdopodobieństwem.
14. W matematyce istnieje kilka wybranych, magicznych stałych, które przecinają wszystkie gałęzie. Te stałe, stale odkrywane w naszej zbiorowej historii, zapewniają infrastrukturę numeryczną w naszym codziennym życiu; tak jak pierwiastki chemiczne w układzie okresowym, specjalne stałe w matematyce są podstawą. Aby wymienić tylko kilka, mamy zero (0), kołowe pi (~3,142), pierwiastek kwadratowy z ujemnej jedynki (i) i oczywiście wykładniczy król, stałą Eulera „e” (~2,718).